Based on the forced bending vibration test, an analytical method and experimental test method for characterizing the dynamic performance of the bolted joint structure based on modal parameters (resonant frequency and damping ratio) are established. Carbon fiber is explored by applying different initial preload and excitation frequency. Time-varying behavior of the pre-tightening of the bolt/epoxy composite bolting and its influencing factors.
The results show that during the 10h vibration fatigue process, the initial pre-tightening force of the bolt is smaller, the excitation frequency is larger, and the pre-tightening force of the joint is more relaxed. The vibration fatigue damage will lead to the deterioration of the joint structure and the increase of damping. The relaxation of the joint is affected by the viscoelasticity of the material and the interfacial friction, of which about 50% of the relaxation is caused by the viscoelastic effect of the composite.
With the realization of various low-cost high-performance composite materials technologies, composite materials are rapidly developing in aerospace, marine, ground vehicles, wind power generation and infrastructure applications. However, due to various stress or temperature environments that are encountered during use, the problem of durability and damage tolerance is becoming the biggest challenge limiting its field of application and scope of use.
In practical engineering, the use of fasteners (rivets, screws or bolts) to assemble the mechanical connection of various structural components is one of the most commonly used forms of connection, and still plays an important role in the development of modern aircraft manufacturing using advanced composite materials. Since the load on the structure of the aircraft is transmitted through the joint, the joint is likely to form stress concentration, which is a weak link of the structure against fatigue damage.
Bickford described in detail the mechanical behavior of the bolted joints, the factors affecting the preload response and self-relaxation, and the design method. It is pointed out that the main cause of the loss of the pre-tightening force of the metal connector can be attributed to time, temperature and vibration.
Under the action of mechanical environment such as impact, vibration and creep, the bolted joint tends to slip, separate or even loose. Especially in the case of low-frequency resonance, the joint is usually a region with large dynamic stress and dynamic strain.
At this time, the deformation energy of the structural vibration is mainly concentrated on the joint portion, which exacerbates the stress relaxation and the local deformation effect, thereby causing the joint to be slack. Therefore, preload tension relaxation is one of the main mechanisms that cause fatigue failure of fastener connection and damage structural integrity.
The long-term durability and performance degradation behavior of structural connections is a comprehensive reflection of the components of the connection system, including various types of joining materials, fasteners, gaskets, sealants, and coatings. Therefore, the cause of the loosening of the connection preload is multifaceted.
An important aspect of the mechanical properties of polymer-based fiber reinforced composites involves the viscoelastic properties of the materials. Viscoelastic materials generally exhibit behaviors such as creep, relaxation, and hysteresis that change over time. In summarizing the design method of composite bolting, Xie Mingji pointed out that due to the viscoelastic behavior of the composite, the clamping force of the fastener will gradually relax with time.
Therefore, the strengthening effect caused by the constraint on the thickness direction must be treated with caution, especially for the long-term use and inconvenient inspection of the bolt connection. The influence of the bolt clamping force relaxation should be considered when determining the allowable extrusion strength.
Thoppul et al. gave a comprehensive overview of several key issues affecting the time-varying behavior of composite bolting preload force relaxation. The time-temperature dependent effects of preload relaxation are highlighted, including modeling techniques and the effects of fatigue and environment on residual strength.
It is emphasized that the clamping force generated by the bolt is different from the metal material connector, mainly depending on the Through-The-Thickness (TTT) performance of the composite connector. Due to the lack of a reinforcing phase in the direction of the plate thickness, the structure is prone to damage and failure, especially in the direction of the plate thickness direction of the polymer matrix.
Therefore, to assess the durability of structural connections, the following critical issues must be understood:
1 How long the initial preload can be maintained after the assembly is connected;
2 How much is the preload loss;
3 How the pre-tension relaxation is affected by the temperature and humidity environment;
4 How the preload relaxation is affected by the external load.
Over the years, many scholars at home and abroad have carried out relevant investigations and studies on these issues from different angles. It can be summarized as two aspects of the moist heat effect and the kinetic effect of the preload tension relaxation.
In terms of the moist heat effect of preloading relaxation, Shivakumar and Crews are pre-tightening the T300/5208 composite in three constant environments: room temperature drying, room temperature environment with water absorption of 0.46% and high temperature drying (66 °C). A 100-day durability evaluation test was conducted.
The results show that the bolt preload force relaxation is 12% at room temperature and high temperature drying, and 14% at room temperature moisture absorption. Obviously, the higher the humidity, the greater the amount of preload relaxation.
Thoppul et al. studied the evolution law of bolt relaxation of three-point bending composite members with bolted joints under static and alternating loads and performed finite element analysis.
The results show that the larger the external load and the higher the frequency, the lower the initial preload and the faster the bolt relaxation. The main reason for the looseness of the bolt under dynamic load is the slippage of the thread and other mechanical thread relaxation mechanisms, not the plastic deformation and viscoelasticity of the material.
In terms of the dynamic effects of preload relaxation, the dynamic response of bolted joints is often more complex than static loads due to strain rate and inertia.
Ibrahim and Pettit systematically expounded the dynamic response and uncertainty of the bolted joint structure, and pointed out that the complexity of the bolted joint problem mainly stems from the uncertainty of the bolted joint structure and its non-smooth and nonlinear dynamic characteristics. .
Under the cyclic external load, the bolt will self-relax, especially under lateral external load, the bolting pre-tightening force will gradually decay with time. When the pre-tightening force decays to a certain critical value, the nut begins to soften.
It is generally believed that the self-relaxation behavior of bolts under dynamic loading is mainly divided into two stages. There is no relative movement between the bolts and the threads in the early stage. The self-relaxation is mainly caused by the cyclic plastic deformation of the thread material, and the latter stage Mainly caused by the relative slip between the nut and the bolt.
Jiang et al. studied the self-relaxation behavior of bolts in the early stage. The test and finite element calculations show that local cyclic plastic deformation occurs near the root of the thread, which produces a cyclic strain ratchet effect, which causes the stress in the bolt to redistribute, which leads to the bolt pre- Tightness creates slack under fatigue loading.
Bhattacharya and other experimental studies have found that the factors affecting the loosening of the bolting preload are not only from the bolt material, but also other fastening components such as nuts or washers and initial tightening torque.
In summary, most of the current researches on the preload force relaxation of bolts mainly focus on the connection interface and the influence of thread slip. In fact, the material to be joined is the main body carried by the joint, and the bolt preload is passed. It is applied by the deformation of the joined material, and thus the viscoelastic properties of the composite will inevitably affect the stress distribution in the bolt, that is, the influence of the material on the preloading relaxation of the bolted joint and the structural performance cannot be ignored.
In this paper, the effects of initial preload and excitation frequency on the time-varying behavior of bolt relaxation are investigated by bending resonance test. The dynamic response of non-joined parts and connectors is compared while considering the influence of frictional slip on the joint interface. To reveal the viscoelastic effect of the composite material that affects the looseness of the bolt, and to more fully understand and understand the mechanism of the preloading relaxation and the influencing factors.
An analytical method for evaluating the dynamic performance of bolted joints based on modal parameters (resonant frequency and damping ratio) is preliminarily established, which provides theoretical basis and technical support for the durability design and application of composite joints.
1. Vibration fatigue test
1.1 Sample and test system
The raw material used for the composite test piece was a prepreg composed of carbon fiber/epoxy resin (T300-7901) (Weihai Guangwei Carbon Fiber Co., Ltd.), and the fiber volume fraction was 67%.
An 8-layer symmetrical orthogonal laminate was prepared by a vacuum hot press (Lin'an Fengyuan Electronics Co., Ltd., MD400-100T-H) by a molding process, and its size was 360 mm × 360 mm × 1 mm.
The test piece is cut into a width of 30 mm, the length L1 of the fixed end is 100 mm, and the length L2 of the free end is taken as three kinds of A, B, and C, respectively, 210, 190, and 170 mm (note: different lengths are set to measure different resonances of the structure) The frequencies correspond to 19.0, 22.0, and 26.4 Hz, respectively, and the total length of the non-connecting members is consistent with the corresponding connectors.
The bolted test piece adopts a single lap joint connection, and the overlapped overlap portion has a length of 20 mm, and the sample structure size is as shown in FIG. In the figure: L3 is the length of the overlapping part of the test piece; L4 is the total length of the non-connecting piece cantilever beam.
The vibration test system consists of a test piece, a clamp, a vibration table, a vibration controller, a power amplifier, an acceleration sensor, a charge amplifier, and a data acquisition system. The schematic diagram is shown in FIG.
The excitation source is the ES-3-150 electric vibration table produced by Suzhou Dongling Vibration Test Instrument Co., Ltd. The excitation is the excitation test object along the thickness direction of the test piece, and the excitation amplitude is monitored by the acceleration sensor on the vibration table.
The data acquisition system uses the DH5929 dynamic strain gauge produced by Jiangsu Donghua Testing Technology Co., Ltd., and the sampling frequency is 200 Hz. The fittings are assembled with M6 bolts and are equipped with a self-contained strain sensor (strain gauges on the copper sleeve for real-time monitoring of bolt preload changes) and standard flat washers.
Figure 1 sample structure size
Figure 2 Vibration test system
Through the calibration test between the sleeve strain and the pre-tightening torque, it is found that the two are basically linear in the range of 2~5N·m preload, and the variation slope k is about 130με/(N·m).
This paper aims to study the influence of the initial preload on the bolt slack in the elastic range, so the initial moment should not exceed 5N·m, and when the initial moment is less than 3N·m, the test data fluctuates greatly. After repeated trials, the initial pre-selection is selected. The applied moment is 3, 4, 5 N·m.
The assembled sample is fixed on the moving structure of the vibrating table by a M8 bolt. The test piece is 40mm higher than the vibrating table. When tightening, the spring washer is used to prevent loosening with a large preload. A strain gauge attached to the surface of the specimen at a distance of 90 mm from the M8 bolt (Aviator Electric Instrument Co., Ltd., BE120-4AA) was used to measure the strain response of the specimen under vibration.
1.2 Test methods
For the detection of the state of the bolted joint, it is difficult to realize by directly measuring the transmission or relative displacement of the force between the two contact faces. The modal parameters (resonance frequency, damping ratio, and modal shape) are functions of structural mass, damping, and stiffness. Therefore, changes in the dynamic properties of the joint structure can be obtained by measuring changes in modal parameters.
The frequency response curve of the sample tested by the sweep vibration test can reveal the softening phenomenon of the bolt structure due to the microscopic slip between the joint interfaces and its elastic state. Schultz and Tsai used the half-power bandwidth method to measure the dynamic storage modulus and damping ratio of fiber reinforced composites by free decay vibration test, and studied the influencing factors of the two.
Schultz and Warwick studied the changes of material stiffness and damping ratio of glass fiber reinforced epoxy composites during vibration fatigue by sinusoidal vibration test. It is believed that the material stiffness decreases and the damping ratio increases due to cracks and other damage during material fatigue. . At present, the method of modal parameters for damage identification of composite materials under dynamic load is mature, but there are relatively few studies on the fatigue performance degradation of joints.
In order to reveal the dynamic characteristics of the preload relaxation problem, the vibration mode test in this test is based on the ASTM E756-05 standard of the American Society for Testing and Materials. The sine sweep test is used to measure the resonance frequency variation of the test piece. In the literature, the free damping method is used to measure the change of the damping ratio of the test piece.
In this paper, a quasi-structure vibration fatigue test method is proposed. The sinusoidal resident vibration fatigue test is carried out on the specimen near the resonance frequency of the specimen (0.3Hz high).
Vibration fatigue refers to the phenomenon that the frequency distribution of the dynamic alternating load (such as vibration, shock, noise load, etc.) of the structure has an intersection or close to the natural frequency distribution of the structure, which causes the fatigue damage caused by the resonance of the structure. It is the fatigue damage caused by the resonance of the structure caused by the repeated load acting on the structure.
Therefore, only the resonance damage caused by the excitation of the structure in or near the resonance bandwidth belongs to the vibration fatigue damage, otherwise it is a static fatigue problem.
In order to meet the above requirements, the vibration fatigue test adopts the loading mode of the sinusoidal resident vibration of the cantilever beam structure. The vibration table excitation system produces the sinusoidal forced vibration of the test piece, the excitation amplitude is always 0.6 mm, and the measurement data is the strain time history.
This test was carried out at room temperature, and each type of sample was repeated 3 times. During the test, three sets of connectors and one set of non-connected parts in the same type of sample simultaneously resonate fatigue. Each type of sample was subjected to vibration fatigue for 10 hours, and was subjected to a modal test test every 2 hours before the vibration fatigue test and after the start.
Modal testing uses sine sweep and free decay vibration. In the modal test, the sine sweep test (4 min each) is used to measure the resonance frequency change of the test piece; the short-term dwell test (1 min each time) is used to measure the change of the damping ratio of the test piece.
Specifically, the sinusoidal resident vibration is applied to the test piece near the resonance frequency of the test piece (0.3 Hz high). After the vibration table stops excitation, the test piece is freely attenuated and the test piece damping ratio can be measured by the half power bandwidth method.
The test flow is shown in Figure 3. After the test piece is installed, firstly use the sine sweep test (sweep range is 15~30 Hz) to measure the first-order resonance frequency (fr) of the four sets of samples: use the strain gauge test to obtain the test. The swept-frequency vibration strain response is obtained by performing Fast Fourier Transform (FFT) transformation on the corresponding variable data to obtain the strain spectrum of each set of specimens. The abscissa corresponding to the highest point of the spectrum curve is its resonance frequency.
Due to processing, installation and structural differences, the resonance frequency of the four groups of samples will be slightly different. In this case, the weight adjustment of the non-joined parts is required (adhesive tape is applied to the free end of the sample) so that the resonance frequencies of the groups are basically the same.
The test piece was subjected to the resident vibration fatigue test near the first-order resonance frequency (0.3 Hz high), so the resident excitation frequencies fe of the three types of samples were 19.3, 22.3, and 26.7 Hz, respectively. The specific test conditions are shown in Table 1.
According to the ASTM E756-05 standard, the dynamic storage modulus of a material is calculated as
Where: Ï is the material density; l is the sample cantilever length; H is the excitation direction sample thickness; Cr is the sample modal coefficient.
Due to the vibration fatigue of the sample, the material density geometry is basically the same, so there is
Equation (2) shows that the change of the resonant frequency of the test piece can be used to know the change of the structural modulus or stiffness.
In this paper, the strain response of the specimen is freely attenuated after the short-term resident vibration is measured, and the amplitude-frequency response function of the specimen is obtained by FFT transformation.
According to the ASTM E756-05 standard, the structural damping ratio is calculated as
Where: f is the first-order natural frequency of the structure; Δf is the half-power formant width of the structure (the bandwidth of the peak range of the 3 dB spectrum is decreased).
2, results and discussion
2.1 Pre-tightening force affects the calibration result of structural dynamic response
In order to calibrate the transient variation of the structural resonance frequency and the damping ratio of the bolted joint under different preloading forces, it provides a basis for the subsequent structural dynamic response analysis. Figure 5 shows the amplitude of the excitation (0.6mm). Resonance frequency and damping ratio of type B connectors under different preloads.
The results show that the damping ratio decreases continuously when the pre-tightening force increases to 5N·m, then the pre-tightening force increases and the damping ratio increases, which means that the pre-tightening force has approached or exceeded the thickness of the connecting material. The compressive yield strength in the direction indicates that it is reasonable to select a pre-tightening force range of 3 to 5 N·m in this test.
At the same time, the comparison of the resonant frequency with the change of the connection pre-tightening force shows that the change trend is not as obvious as the damping ratio. This indicates that the change in the detected structural damping ratio is more effective than the detection of the resonant frequency to reflect the pre-tightening state of the bolted joint.
2.2 Influence of excitation frequency on bolt slack
Figure 6 is a time history curve of the preload force relaxation of composite joints at different excitation frequencies.
6(a) to 6(c) correspond to excitation frequencies of 19.3, 22.3, and 26.7 Hz, respectively. The data of each group in the following similar test pieces are represented by the average value. The time history of preload relaxation is expressed as P/P0, where P0 is the initial preload and P is the bolt preload force detected in real time.
It can be seen from the comparison in Fig. 6 that the smaller the initial preload force at the same excitation frequency, the greater the loss of the connection preload force with time. This is because the greater the preload force, the greater the pressure at the joint contact surface, and the greater the friction force that is required to overcome the tangential force of the slack, so that the joint is less prone to slack.
At the same time, at lower excitation frequencies (19.3 Hz and 22.3 Hz), the difference in the looseness of the bolted joints under different initial preloads is small, while at 26.7 Hz, the difference in the degree of relaxation of the three preloading forces tends to increase significantly. .
The statistical results of the preload force relaxation amount after 10 hours of the test at each excitation frequency are shown in Table 2. In the table: Φf and
It is the coefficient of influence of viscoelasticity of composite materials. According to the initial preload force, the average slack is about 1.1%~2.5% at 19.3Hz; the average slack is about 2.9%~3.9% at 22.3Hz; the average is at 26.7Hz. The amount of relaxation is about 3.4% to 7.7%.
The comparison results also show that the initial preload force at different excitation frequencies has a consistent effect on bolt slack.
The evolution of preload relaxation with time (t), and the Shivakumar-Crews model of the literature
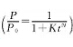Very consistent (where K and N are material constants), showing a significant power function variation. 0 
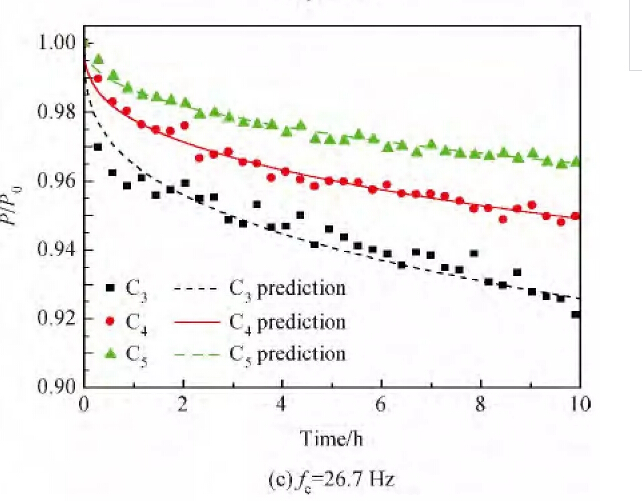
Fig.6 Time history curve of preloading relaxation of composite joints under different excitation frequencies
2.3 Effect of initial preload on bolt slack
Figure 7 is a time history curve of the preload force relaxation of composite joints under different initial preloads. 7(a) to 7(c) correspond to the initial preload forces 3, 4, and 5N·m, respectively.
Among them, when the initial preload is 3N·m, the average relaxation of 10h at the three excitation frequencies is about 2.5%~7.8%; at 4N·m, the average relaxation is about 1.2%~5.1%; at 5N· At m, the average relaxation amount is about 1.1% to 3.4%.
The comparison shows that at the same pre-tightening force, the higher the excitation frequency of the test piece, the faster the bolt pre-tightening force relaxes. This is mainly because the higher the excitation frequency, the greater the strain rate of the test piece.
At the same time, the more the number of cycles per unit time, the more energy the friction consumes, and the higher the excitation frequency, the faster the bolted test piece relaxes. In addition, under the initial small preload (3N·m and 4N·m), the difference in the degree of relaxation caused by the difference in excitation frequency is large, and the difference is relatively reduced under the preload of 5N·m. .
2.4 Connection structure dynamic response analysis
The preload tension relaxation reflects the energy dissipation process of the structural system during the vibration process. The internal resistance of the material and the dry friction between the structural components are the main sources of energy change. Structural dynamic response is closely related to the evolution of material microstructure. Therefore, it is important to clarify the inherent dissipation behavior of materials as an indicator of preload tension relaxation.
In this paper, the resonance frequency and the damping ratio are used to characterize the dynamic response. The influence of the dynamic response of the viscoelastic composite on the preload relaxation is analyzed by comparing the joint and the non-connected parts.
Figure 8 is a graph showing strain spectrum changes around the first-order resonance frequency over different time periods measured during the test of the Type B connector. It can be seen that as the test time increases, the resonance frequency of each time period shows a gradual decrease trend compared with the initial stage of the test.
Among them, the 3N·m pre-tightening test piece (see Figure 8(a)) has a resonance frequency (fr0) of 22.115 Hz before the test, and the resonance frequency (fr10) decreases to 22.013 Hz after the test for 10 hours, and the relative change amount is -0.102 Hz. The resonance frequency changes of 4N·m and 5N·m pre-tightening connectors and non-connecting parts are -0.098 Hz (see Figure 8(b)), -0.064 Hz (see Figure 8(c)) and -0.059 Hz ( See Figure 8(d)). Table 2 lists the statistical results of the structural resonance frequency changes of various types of specimens after 10 hours.
Figure 9 shows the time history of the resonance frequency of various types of specimens extracted from the strain spectrum variation curve (Fig. 8). The straight line is the result of linear regression analysis for each test data. As can be seen:
1 The resonant frequency of the connecting piece and the non-connecting piece gradually decreases with the fatigue caused by the vibration;
2 In terms of the resonance frequency drop gradient, the non-connecting member is significantly lower than the connecting member, and the smaller the pre-tightening force, the tendency of the resonant frequency variation gradient to increase;
3 The resonance frequency falling gradient is directly related to the excitation frequency. The larger the excitation frequency, the more the resonance frequency decreasing gradient tends to increase.
As can be seen from equation (2), a change in the resonant frequency means a change in the stiffness of the material. The decline of the stiffness of the non-joined parts is mainly caused by the fatigue of the material itself: the viscoelasticity of the matrix and the cracks in the interface between the matrix and the fiber with fatigue; and for the joints, the fatigue damage of the material, the friction of the interface and the fatigue of the bolted joint structure Softening causes stiffness decay.
It can be seen from the above results that the relaxation of the composite bolted joint in the vibrating environment is mainly caused by the synergistic effect of the viscoelasticity of the composite material and the interface slip, wherein the structure of the viscoelastic composite material itself is degraded during the pretensioning of the connecting member. The effect of stiffness decay cannot be ignored.
For the connecting piece, the smaller the initial preload, the greater the degree of looseness of the bolt, and the faster the stiffness of the joint is decayed. The higher the excitation frequency, the higher the strain rate of the test piece, the more heat is generated per unit time, and the joint is pre-tensioned. The faster the force is relaxed, the faster the specimen stiffness decays.
Figure 10 is a graph showing the damping time history. The straight line is the result of linear regression analysis for each test data. It can be seen from the variation of the damping ratio of the specimen under different excitation frequencies:
1 The damping ratio of the connecting piece and the non-connecting piece gradually increases with the vibration fatigue.
2 The damping of the non-connecting parts is lower than that of the connecting parts, and the larger the pre-tightening force, the smaller the damping ratio of the connecting parts. This is because during the vibration process, the connection interface is dissipated by the additional energy due to the friction, and the damping ratio is correspondingly increased.
3 The rate of damping change of non-connected parts is relatively stable. When the composite material vibrates, the initiation crack in the matrix, the interface between the matrix and the fiber, and the fracture of the fiber material will lead to an increase in the internal damping of the material.
Comparing the damping ratio of the connecting piece and the non-connecting piece under the similar test piece, the structural damping of the connecting piece is mainly composed of the internal damping of the composite material, but the variation trend of the structural structure damping is different from that of the non-connecting piece, which is mainly caused by the bolt connection part. Due to the complex energy dissipation mechanism, the existence of frictional damping makes the connection damping change an unstable trend.
Figure 9 Resonance frequency time history curve
Figure 11 shows the wear of the joint interface of the composite connector. It can be seen that after 10h test, the contact surfaces are worn due to the relative frictional slip, wherein the circle (â—‹) indicates the wear between the connecting plate and the gasket, the box
The inside of the connecting hole is marked for wear. 
Figure 10 Damping ratio time history curve
It can be seen from Fig. 11 that the wear distribution is obviously affected by the initial preload: the surface contact wear area between the connecting plate and the gasket expands as the initial preload force increases, and the wear inside the connecting hole shows The pre-tightening force increases and decreases.
The influence of the initial preload on the wear area mainly reflects the relationship between the bolt connection load distribution and the transmission mechanism. When the pre-tightening force is large, the pressure between the contact faces is also large enough, and the connection load is mainly transmitted by the frictional force between the connecting material and the gasket, so that the surface of the connecting plate is largely worn;
When the pre-tightening force is small, the pressure combination between the contact faces is weak, so the connection load is mostly transmitted by the contact between the bolt and the hole, so that the inside of the connecting hole generates a large amount of wear marks; and when the medium preload is applied, The joint load is transmitted both by the surface friction and by the contact collision between the bolt and the hole, so that the surface contact area and the contact area in the hole have different degrees of wear.
The difference in the initial pre-tightening force causes the degree of frictional slip between the contact faces of the connecting members to be different, thus causing a difference in the pre-tightening force of the connecting members.
The loss of the connection preload during the vibration process can be attributed to the stress redistribution caused by the stiffness attenuation of the bolt and the joint material under the vibration load. To better analyze the looseness mechanism of the joint, Figure 12 shows the looseness of the bolt and the connected material. Schematic diagram of load analysis before and after.
After the pre-tightening force is applied to the static lower connecting member, the length of the bolt is deformed to ΔL0, and the thickness of the connecting material is deformed to ΔT0, and tan θB and tan θJ are the rigidity of the bolt material and the connecting material, respectively, under the action of the initial pre-tightening force FP. The tension between the tension in the bolt and the pressure of the connecting member; when the connecting member is subjected to the vibration load, the length of the bolt is deformed to be ΔL, the thickness of the connecting material is deformed to ΔT, the resultant force of the tension FB of the bolt and the pressure FJ of the connecting material It is equal to the excitation load Fz.
Since the excitation load Fz is a periodic dynamic load, it can be known from the equilibrium relationship that the tension FB of the bolt and the pressure FJ of the connecting material also periodically change, and the magnitudes of the changes are ΔFB and ΔFJ, respectively.
It can be seen from the above analysis that after a long time of vibration, the stiffness of the fastener and the connecting member will be attenuated, and the composite material will creep. In order to achieve a new equilibrium relationship, ΔFB and ΔFJ are correspondingly changed, thereby causing bolts and connecting materials. The redistribution of stress, which in turn causes the preload of the connector to degrade to F'P.
Therefore, the plastic deformation of the thread and the viscoelastic dynamic effect of the composite cause stress relaxation in the thickness direction of the material, and the synergistic effect of the two causes the connection preload to relax. These mean that the effect of the viscoelastic properties of the composite on the looseness of the joint cannot be ignored.
Interfacial friction and viscoelastic effects of the composite will cause the preload to relax, resulting in a decrease in the structural resonance frequency.
By comparing the difference between the rate of decrease of the resonant frequency of the non-connecting member and the connecting member, according to formula (4), the influence of the viscoelastic effect of the composite on the slack of the connecting member can be evaluated, and the coefficient is defined as
Where: fm is the rate of change of the resonant frequency of the non-connecting member; fj is the rate of change of the resonant frequency of the connecting member.
The statistical results are shown in Table 2. The analysis shows that the relaxation of composite bolted joints is affected by the viscoelasticity and interfacial friction of the material, about 70% of which is caused by the viscoelastic effect of the composite, and the initial preload force affects the composite. The proportion of influence of viscoelasticity.
Since fm in equation (4) is the rate of change of the overall resonant frequency of the non-connected member, it is not the rate of decrease of the structural resonance frequency caused by the fatigue of the material in the local joint region, and thus the calculated influence coefficient is high.
In order to further evaluate the effect of the viscoelasticity of the composite on the looseness of the joint, an effective extraction method for the internal resistance of the joint and the dry friction damping in the local area of ​​the joint is considered.
Assuming that the difference between the damping ratio of the connecting piece and the non-connecting piece comes from the dry friction of the connecting contact portion, the dry friction damping ratio of the connecting piece can be defined as
Where: γjP is the structural damping of the whole connecting member under the pre-tightening force P; γm is the corresponding non-connecting member damping ratio.
Assuming that the composite damping is uniformly distributed with the volume, the effective internal damping ratio of the lap joint composite can be defined as
The damping ratio can be used to estimate the effect of the viscoelasticity of the composite on the looseness of the joint. The coefficient is defined as
Calculate the modal damping data measured every 2h in the 10h vibration fatigue test by using equation (7), obtain the corresponding coefficient Φγ, and then calculate the viscoelastic influence coefficient of the composite by the average method.
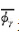(See Table 2). The analysis shows that about 50% of the preload force relaxation caused by the change of structural damping is derived from the viscoelastic effect of the composite. The results also show that at the same frequency, the higher the initial preload, the above influence coefficient also tends to increase.
3. Conclusion
(1) In the 10h test time, the larger the initial preload force, the smaller the bolt relaxation under the same excitation frequency; under the same initial preload, the larger the excitation frequency, the greater the bolt preload force relaxation.
(2) The preload force loss of the joint during vibration fatigue reflects the decrease of the resonant frequency of the connected structure and the energy dissipation law of the increased damping.
(3) The vibrational relaxation characteristics of composite bolted joints are synergistic effects of creep-slip and thread interface friction of the joint material, of which about 50% depends on the viscoelastic behavior of the composite. The difference between the metal material and the composite connection structure needs further study.
Piston Ring is a metal Ring used to insert the inner Piston groove,
Piston Ring is divided into two types: compression Ring and oil Ring
1,Compression Ring can be used to
seal the combustion chamber combustible mixture of gas;
2,The oil ring is used to scrape excess oil from the cylinder
Piston ring role includes sealing, oil regulation (oil control),
heat conduction (heat transfer), guide (support) four roles.
Packing Ways:
A. Neutral Packings
B Dwit Brand Packings
C. Meet customers' demand
A. By sea (please let us know your destination port )
B. By air (please let us know your air port )
C. By express (please let us know your detail address , post code )
D. By your agent (if your agent in Guangzhou , we can send to them by free accordingly )
PS: we can supply you detail documents (B/L. CO, CIQ, Commercial invoice, Packing list etc.)
for Customs clearance as you demand
Diesel Piston Rings,83Mm Piston Ring,Piston Ring For Mercedes Ben,Engine Piston Rings
Shijiazhuang Longshu Mechanical & Electrical Equipment Trading Co., Ltd. , https://www.lsjgbearing.com